Measuring early or late dependence for bivariate lifetimes of twins

Abstract

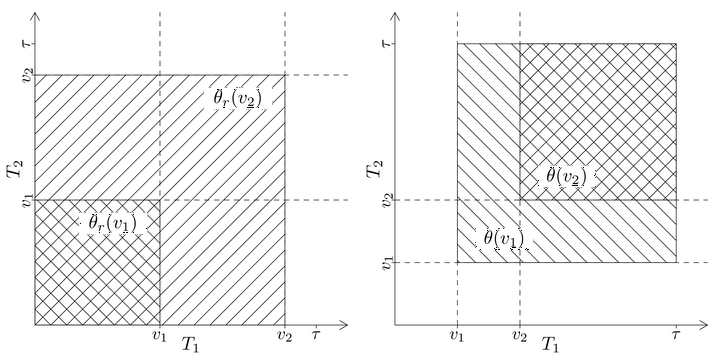
We consider data from the Danish twin registry and aim to study in detail how lifetimes for twin-pairs are correlated. We consider models where we specify the marginals using a regression structure, here Cox’s regression model or the additive hazards model. The best known such model is the Clayton-Oakes model. This model can be extended in several directions. One extension is to allow the dependence parameter to depend on covariates. Another extension is to model dependence via piecewise constant cross-hazard ratio models. We show how both these models can be implemented for large sample data, and suggest a computational solution for obtaining standard errors for such models for large registry data. In addition we consider alternative models that have some computational advantages and with different dependence parameters based on odds ratios of the survival function using the Plackett distribution. We also suggest a way of assessing how and if the dependence is changing over time, by considering either truncated or right-censored versions of the data to measure late or early dependence. This can be used for formally testing if the dependence is constant, or decreasing/increasing. The proposed procedures are applied to Danish twin data to describe dependence in the lifetimes of the twins. Here we show that the early deaths are more correlated than the later deaths, and by comparing MZ and DZ associations we suggest that early deaths might be more driven by genetic factors. This conclusion requires models that are able to look at more local dependence measures. We further show that the dependence differs for MZ and DZ twins and appears to be the same for males and females, and that there are indications that the dependence increases over calendar time.