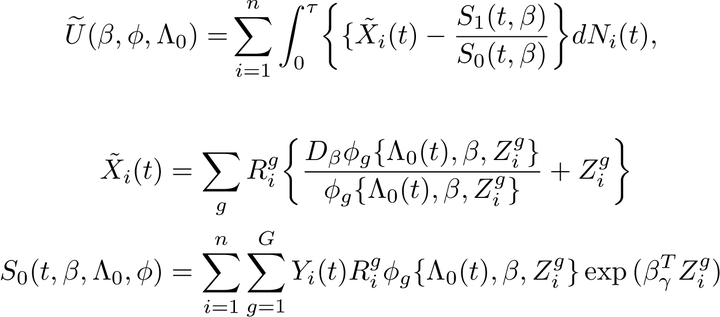
Abstract
Missing covariate values is a common problem in survival analysis. In this paper we propose a novel method for the Cox regression model that is close to maximum likelihood but avoids the use of the EM-algorithm. It exploits that the observed hazard function is multiplicative in the baseline hazard function with the idea being to profile out this function before carrying out the estimation of the parameter of interest. In this step one uses a Breslow type estimator to estimate the cumulative baseline hazard function. We focus on the situation where the observed covariates are categorical which allows us to calculate estimators without having to assume anything about the distribution of the covariates. We show that the proposed estimator is consistent and asymptotically normal, and derive a consistent estimator of the variance–covariance matrix that does not involve any choice of a perturbation parameter. Moderate sample size performance of the estimators is investigated via simulation and by application to a real data example.